Coupled analysis improves deepwater spar riser and mooring design
Development of deepwater fields requires complex systems for production and export of oil and gas. These can include combinations of steel catenary risers, flexible flowlines, top tensioned risers, and hybrid risers, connected to one or more moored floaters such as spars, tension leg platforms, semisubmersibles, and ships. The floater may be moored with either catenary or taut legs.
The surge motion of floaters in deepwater occurs predominantly at the resonant period of the moored system, which is typically in the range of 2-5 minutes. For spars, pitch motion is also dominated by the resonant response, which occurs typically at periods of 40-100 seconds.
As water depth and number of risers increase, damping due to drag on the mooring lines and risers dominates these resonant low-frequency motions. This, in turn, impacts the design of the risers and moorings. It is essential to use coupled floater/mooring/riser dynamic analysis to model the damping.
This article illustrates the importance of coupling effects for a spar platform with taut-leg mooring in a water depth of 6,000 ft. Practical application of coupled analysis in combination with calibrated linear models is also described.
Low frequency response
The low frequency motion responses of floating structures are generally lightly damped, resonant responses. When the damping is small, the standard deviation of the motion,sx, can be approximated by the following formula:where SF(vn) is spectral density of the combined wind and wave drift load at the natural frequency, "c" is the stiffness and "b" is the damping coefficient. Fatigue damage is proportional to the fourth power of the motion, making it inversely proportional to the square of the damping. An accompanying figure illustrates the motion and fatigue damage sensitivity to the amount of damping.
Linear vs. coupled analysis
Traditionally, the motion response of moored floating structures has been calculated by representing the moorings and risers as massless linear springs. The shortcoming in this "separated" linear approach is that the inertia, damping, and stiffness of the mooring and risers as well as the mean current loads acting on them are not fully considered when calculating the floater motions. In particular, it is not practical to estimate the viscous damping arising from drag on the mooring lines and risers.
In coupled analysis, the risers and mooring lines are included in the model along with the floater. In this way, damping of the floater motion due to drag on the mooring lines and risers is incorporated directly.
Coupled analysis
The coupled analysis described in an example below was performed using Stress Engineering Services' own RAMS (rational approach to marine systems) software. RAMS was designed to produce results needed by riser and mooring designers. The coupled analysis capability in the frequency domain is an essential feature for performing iterative design calculations because it runs faster than time domain analysis. A final design should be verified in the time domain so that important nonlinearities can be accounted for, and RAMS includes this capability.
The program uses a finite element representation of an elastic rod to model risers, tension leg platform (TLP) tethers, and mooring lines. This element includes axial and bending stiffness. The external load model accounts for weight, buoyancy, internal fluids, and hydro dynamic loads. A generalized Morison model is used to compute hydro dynamic loads.
Seabed contact is simulated by nonlinear spring and friction models. The finite element method uses a displacement formulation that allows for large element displacements and rotations in three-dimensional space, while strains are assumed to be moderate.
One or more floaters may be included in the analysis. Each floater is represented by a rigid body with six degrees of freedom, which is introduced into the finite element model as a nodal component. The load model for the body accounts for wind, wave, and current forces. First and second order wave force coefficients are obtained using a diffraction/radiation solver such as Wamit or Wintcol. Dynamic wind and slow drift loads are calculated in a preprocessor. A convolution integral is used to represent radiated wave effects in the time domain.
Lightly damped resonant responses are narrow banded. Consequently, it is essential to allocate appropriate frequency spacing in order to capture the response. The software's preprocessor allows for efficient generation of the frequency spacing. It includes a number of wave and wind spectral forms, steady user-defined shear currents, and the ability to model an uneven seafloor.
Calibrated linear model
Results from a coupled analysis can be used to define stiffness and damping matrices for the rigid body that represent the stiffness and damping of the mooring lines and risers. This calibrated linear model can be very useful for conducting riser and mooring design calculations. The predicted motions will be adequate as long as the system configuration and environmental conditions don't change much from those used in the calibration.
In general, a calibrated linear model may be obtained from the fully coupled model results by (1) neglecting the mass of the mooring lines and risers, (2) developing six-by-six stiffness matrices from the fully coupled run using the secant stiffness for the static response and the tangent stiffness at the mean offset position for the dynamic response, and (3) assuming Rayleigh damping. The calibration is performed by adjusting the damping factors to match the fully coupled response.
The calibrated linear model represents an improvement to the conventional riser and mooring leg design approach in which floater motions are imposed as a constraint to the model of a single riser or mooring leg. The calibrated linear model represents a portion of the floater/mooring/riser system, while allowing detailed nonlinear representation of one or more of the remaining components, thereby allowing feedback between the models. The approach is equivalent to the super-element concept common in structural analysis software.
The following illustrates how this approach could be used in design. An important design parameter for a spar is the location of the mooring fairleads. Careful placement can reduce pitch-induced fatigue loads on the risers at the keel. The steps involved are:
- Select the risers and riser pretensions.
- Model the mooring and all the risers except the most upstream and most downstream (which are most susceptible to fatigue).
- Develop a calibrated linear model using results from a fully coupled analysis.
- Add full models of the upstream and downstream risers to the linear model.
- Run a (reduced) scatter diagram and calculate the fatigue life of the upstream and downstream risers.
- Select another fairlead attachment point.
- Repeat Steps 2 through 5.
- Calculate the mooring attachment that should provide maximum fatigue life for the risers.
Another illustration is the addition of a catenary riser to the spar. A calibrated linear model could be developed, a complete model of the catenary riser attached, and the fatigue life checked. Since there are two parameters to select (connection height and horizontal tension), a set of cases can be run and the best combination selected.
Spar in 6,000 ft depths
The example spar is 122 ft in diameter, has a draft of 650 ft, and has a displacement of 53,000 tons. The taut-leg mooring system consists of 14 legs uniformly spread. Mooring legs consist of wire rope terminated with short chain segments at both the platform and anchor. A description of the mooring line composition is given in an accompanying table. The spar supports a total of 22 risers having a total top tension of 26,000 kips. An elevation view of the spar, mooring, and risers is shown in an accompanying diagram
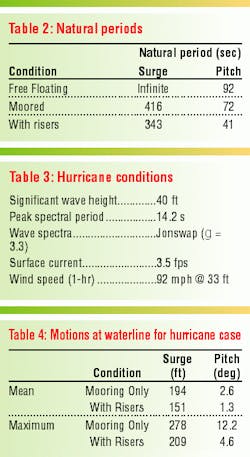
The mooring and risers affect the surge and pitch natural periods. Table 2 gives the undamped natural periods for the free-floating spar and for the moored spar without and with risers. The riser top tension has a significant effect on both the surge and pitch natural periods.
The hurricane metocean conditions used are listed in Table 3. Table 4 presents the computed mean and maximum surge and pitch motions at the mean water line. The presence of the risers significantly reduces both the surge and pitch motion. The mean surge and pitch are reduced because of the increase in stiffness that results from the riser top tension. The dynamic surge and pitch are reduced due to both the addition of riser stiffness and the increase in viscous damping.
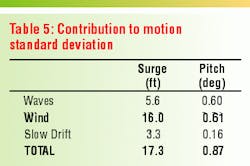
Table 5 shows the relative contribution to the dynamic surge and pitch. The wind dominates the dynamic surge and has about the same contribution to the dynamic pitch as the waves. As discussed, for riser and mooring design purposes, it is desirable to be able to develop a calibrated linear model from the results of a fully coupled model simulation. Table 6 compares the calibrated linear model responses with those from the coupled analysis. The calibrated critical damping factors are 4.4% for pitch and 20.6% for surge. The excellent agreement shows the validity of the calibration procedure.
The calibrated linear model concept has much potential for improving riser and mooring fatigue calculations. This can be particularly useful for riser design, which is frequently controlled by fatigue. Consequently, it is of interest to illustrate that a linear model can be calibrated for lower seastates as well. A coupled analysis was performed using a 5 ft significant wave height with 6 second peak period and a wind speed of 15 knots.
Table 7 shows how the calibrated linear model responses compare with those from the coupled analysis. The calibrated critical damping factors are 1.3% for pitch and 1.5% for surge. As for the hurricane response, the agreement is excellent.
The mooring and risers significantly affect the motions of a spar in deepwater. Mooring and riser stiffness affects the natural periods and the motion amplitudes. Viscous damping due to drag on the mooring lines and risers significantly affect the motion amplitudes. These effects in turn impact the design of the risers and mooring. Coupled analysis is needed to provide a consistent way for modeling these effects, particularly the damping.
Accurate representation of the damping is critical for fatigue sensitive riser components such as those located at the keel section of a spar. Calibrated linear models can be very useful for riser and mooring design and parameter studies. However, they must be calibrated using results from coupled analysis.
References
Faltinsen, O., "Sea Loads on Ships and Offshore Structures," Cambridge U. Press. 1990.
Garrett, D., "Dynamic Analysis of Slender Rods," J. of Energy Resources Technology, ASME, Vol. 104.
Acknowledgement
The authors wish to thank Thomas Black of Stress Engineering Services, instrumental in the development of RAMS, and Ronald Reagan (formerly with SES) for his significant contribution to RAMS development.