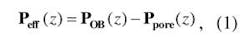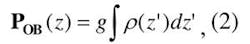Assessing the risk of drilling hazards using seismic uncertainty analysis
Konstantin Osypov
Yi Yang
Ran Bachrach
Cengiz Esmersoy
Schlumberger
Drilling, particularly in the deepwater environment, is becoming increasingly complex and expensive. A significant portion of all total non-productive time in deepwater is due to abnormal geopressures. This manifests itself in situations such as blowouts, stuck pipe, losses, and wellbore instability. This in turn can lead to severely extended drilling programs, significant cost overruns, abandonment of wells, and in the worst cases, loss of capital equipment and potentially loss of life. Pre-drill assessment of geohazards has, therefore, become an essential component of well planning. The behavior of rock velocities with depth is related to the state of shale dewatering and compaction and, consequently, the pore pressure that can be expected at depth. Quality seismic data and velocity is therefore the key to pore-pressure prediction.
However, as velocity estimation from seismic data is not unique, incorporation of velocity uncertainty in drilling risk analysis can yield a better understanding of the range of potential pore pressures. Quantification of velocity and correspondingly geopressure uncertainties is therefore essential in decision making before and during drilling operations. In particular, decisions for casing points and mud programs should take into account the geohazard risk associated with the uncertainty in our knowledge of the velocity model. Pre-drill work may also help define the measurements needed to adequately constrain the velocity uncertainties in key sections of the well. The goal here is to introduce workflows for pore-pressure and fracture-pressure prediction that account for uncertainties associated with the ambiguity of tomographic velocity model building.
Understanding geohazards
Drilling through geohazards, like overpressured zones, poses significant risk and, as such, mitigation and prevention are paramount. This demands improved understanding of geohazards, their preconditions, causes, and implications. Specifically, anomalous pore pressure is considered to be a major geohazard whose prediction is needed for well planning. Common pore-pressure mechanisms are compaction disequilibrium and smectite-to-illite diagenesis. When drilling a well, knowledge of the pore pressure and the fracture pressure is used to plan a mud-weight pressure window, which can be used to decide the depth of casing points. For safe and cost-effective drilling, it is crucial to have estimates of the pore-pressure and fracture-pressure distribution in the subsurface, and also to localize these geohazards before drilling.
Estimates of the pore pressure and the fracture pressure can be obtained from information on the variation in compressional wave velocities in the subsurface by using empirical pore-pressure prediction models. These methods are based on Terzaghi's effective stress principle that states that all effects of stress on measurable quantities (such as compressional-wave velocities) are a function of the effective pressure:
where Peff(z) is the effective pressure at depth z, Ppore(z) is the pore pressure at depth z, and POB(z) is the pressure due to the overburden at depth z. Further:
where g is the acceleration of gravity, ρ(z) is bulk density, and the integration is carried out from the surface to depth z. Pore pressure can be estimated using Eaton's equation:
where Pnorm(z) is the normal (hydrostatic) pore pressure, V(z) is the compressional-wave velocity, and Vnorm(z) is the normal value of velocity expected when there are no overpressures. Eaton originally suggested that the exponent, n, should be around three. However, Bowers noted that, if overpressures are the result of mechanisms other than under-compaction, the appropriate value of n should be higher (up to about five). The above equations assume 1D vertical relationships. However, Terzaghi's principle can be extended to 3D. In that case, 3D basin geomechanical modeling is necessary. If basin modeling is not using seismic velocities, then Terzaghi's principle could be used in reverse order to provide prior information on seismic velocities from an effective stress model. Also, note that an anisotropic rock model can be used to utilize an anisotropy estimate to better constrain pore pressure under a compaction disequilibrium assumption.
Common practices for pore-pressure prediction (PPP) from seismic measurements are deterministic, i.e., one PPP volume is calculated from one volume of seismic velocities. However, even with our best efforts to combine all available data, there is still ambiguity in our velocity models caused by the inherent non-uniqueness of inversion. Many different seismic velocity models can match the observed seismic data equally well, within the tolerance of measurement error, and this ambiguity grows rapidly away from known control points such as well logs. This also results in uncertainty in the true positions of anomalous geopressure zones interpreted from seismic. These uncertainties lead to drilling risks. While the underlying ambiguity can never be fully eradicated, a quantified measure of these uncertainties provides deeper understanding of the risks and leads to more informed decision making and economic savings. Additionally, these estimates may be updated as the wellbore is being drilled and new information is acquired.
Uncertainty in pore pressure can be quantified for a given model by exploring the dependency of the predicted pore pressure to the uncertainty in the input velocity field and model parameters. Doyen and Sayers used a Bayesian approach to propagate input velocity uncertainty into final uncertainty in pore-pressure prediction. The method can be used to estimate pore-pressure uncertainty before drilling, but also one can utilize the new information obtained from well logs while drilling (e.g., checkshot information) to update the pore-pressure prediction. Osypov et al. introduced a new method for seismic velocity uncertainty analysis based on sampling the posterior distribution of the anisotropic tomography operator constrained by wells, geology, and rock physics. The resultant models are all valid solutions to the original tomography problem; they all fit the travel time measurements to within the noise level and satisfy the original prior information and geological constraints. This method is applied to the sampling of the posterior probability distribution for pore-pressure estimation.
Methodology
The workflow for geohazard prediction is as follows:
- Start with a tomographic tilted transverse isotropy (TTI) velocity model, a seismic image, and image gathers
- Generate velocity model samples (500-1,000 models) from the posterior distribution by using an eigendecomposition of the anisotropic tomography operator and null-space projection
- Perform statistical analysis of velocity volumes and anisotropy parameters to generate corresponding uncertainty volumes
- Apply rock-physics transformation to each velocity model from the ensemble from Step 2 to generate estimated pore pressure, fracture pressure ensembles, and corresponding uncertainty volumes
- Optionally, for selected interpreted geohazard objects, perform 500 map re-migrations for the models from Step 2 and generate uncertainty volumes for their locations (P10, P50, P90 volumes).
Well measurements beyond surface seismic can be employed in the analysis and further reduce the uncertainty. There are two ways of incorporating well information. One way deals with re-doing uncertainty analysis for a new tomography operator combining seismic data and new well measurements. Another way deals with a sifting process. The objective for sifting is to update the set of allowable models as we drill a well so that they are consistent with the new information. One option for sifting is based on updating the set of posterior models as we drill so that they are consistent with new depth measurements to marker horizons, i.e., as we drill the well, we only keep those posterior models where the marker horizon depth matches the well measurement within a given bound (we must allow for well depth errors and others). The population of models will become smaller as we pass each marker horizon because the set of models is sieved by the new knowledge. An alternative and complementary option is to sift the models with checkshot data. As we get a new checkshot time, we only keep those models that match the time within an allowed error. For both options, uncertainty of velocity, pore pressure, and fracture pressure decreases, in particular ahead of the bit, as we cull the population of models. This property reflects a Bayes' principle in which adding new information reduces the degrees of freedom in an inference problem, and with it, the uncertainty. One nice feature of sifting workflows is that we do not need to update the velocity model. We only must have access to the precomputed set of, for example, 500 models, horizons, and associated pore-pressure and fracture-pressure realizations. A disadvantage of sifting is that the updated uncertainty may be underestimated if the number of acceptable models becomes too small, e.g., there will be no apparent uncertainty when the number of models is reduced to just one.
Case study
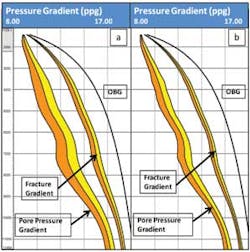
A case study was conducted in the Green Canyon area of the Gulf of Mexico. In this case, 3D seismic data in the area were processed without well data, resulting in velocity and pore-pressure estimates with uncertainties. Five hundred anisotropic models were generated with the workflow above. Figure 1 shows four sample vertical extractions at the well location out of 500 3D velocity volumes, together with corresponding pore pressure and fracture gradient depth profiles after applying the rock-physics transformation to each individual velocity profile. Figure 2 (a) presents the P10-P50-P90 range of velocity based on the 500 realizations. Figure 2 (b) presents the P10-P50-P90 ranges for pore-pressure gradients and fracture gradients after applying the rock-physics transformation of Eaton with Exponent 3 to each velocity realization. In particular, the reduction in P10-P90 ranges for pore-pressure gradients and fracture gradients effectively widens the mud-weight pressure window, which is crucial in deciding the depth of casing points. The reduction of pressure uncertainty is coming from the information content from surface seismic measurement.
Conclusions
Drilling into unanticipated geopressure in permeable sands or carbonates can cause major blowouts, and in comparatively impermeable shales, routinely raises a range of wellbore stability issues. As oil and gas targets become deeper, it becomes more important for drilling engineers to understand pressure environments to properly place well casing points, because even one misplaced casing may result in a failure to reach target depth. Furthermore, understanding geopressure uncertainty allows mitigation of drilling risks. Therefore, quantification of geopressure uncertainty is essential in well design and drilling operations. The authors introduced workflows for the statistical analysis of pore-pressure and fracture-pressure uncertainty associated with the ambiguity of tomographic velocity model building. The approach also enables analysis of the geopressure uncertainty associated with rock-physics modeling by applying various rock-physics transformations to the velocity ensemble and then combining the resultant statistics. Also, in application to seismic guided drilling, the geopressure uncertainty and associated risks can be updated in real drilling time using the described sifting strategy.