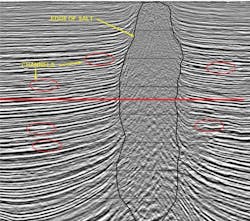
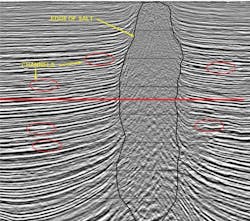
Breakthrough in basin modeling using time/space frame

The workflow to construct the UVT model is as follows:

1. Interpret the faults and of the main stratigraphic events from the seismic data in the XYZ space

2. Build a stratigraphic column, listing the considered stratigraphic events and their relationships

3. Compute 3D UVT parameterization of the volume constrained by the given faults, the stratigraphic events and the stratigraphic column.

The advantages of the UVT space for this workflow are numerous:

• The UVT transform is computed on top of an unstructured mesh which honors the fault network. Layers on each side of the fault can glide along the fault surface as required for proper restoration. In addition, the finite element mechanical restoration accepts various types of grid (hexahedra, tetrahedra, prism). Since the UVT model consists of a set of UVT tetrahedrons, the finite element mechanical restoration can share the same unstructured mesh element. Sharing existing grids gains time and simplifies workflow. The creation of the finite element mesh has been the bottleneck in 3D restoration. Fault transmissivity depending on the displacement of the fault, which varies through time, can be computed automatically.
• The UVT transform is computed for all stratigraphic sequences independently. Further, the eroded part of the sequence is computed to ensure continuity in case of partial erosions of the structure. The UVT transform contains information to represent layer tops that have been eroded through time. Paleo-maps of horizons before erosion, including fault displacement, can be created. In addition, it is possible to “add back” some material, estimate volume before erosion, and restore so that the eroded layer can be restored.
• The continuous UVT transform can be discretized into grids using different techniques, but, importantly, always linked to the UVT space. As the unstructured mesh carrying the UVT transform is restored, all objects created in the UVT transform will be restored. That is, the “magic” of the UVT transform. Because the evolution of the UVT transformation is described in 4D, location of cells can be tracked through time.

Example of a ‘hybrid’ grid honoring the fault surfaces and the stratigraphic while mainly composed of hexahedral cells.

However, restoration is not done with the UVT transform. Although the UVT transform computes a flattened space, this space is not a “true” restored space. The restoration is computed through a finite-element mechanical code, that allows for sliding fault blocks on fault surfaces and minimizes elastic deformation of the rock so the top of the layers reaches a (typically flat) target surface.

Gridding

The new generation of basin modeling simulation software (and other similar simulation engines) requires grids which:

1. Follow the stratigraphy

2. Have mostly cubic (hexahedral) cells

3. Have cell faces parallel to the fault surfaces

4. Cells against faults need to be “nicely degenerated” from hexahedra to pyramids, wedges, and tetrahedra.

These requirements are met by so called 2.5D grids (pillar grids). Pillar grids cannot handle the complex faulting required to model sedimentary basins. A UVT model can be constructed inside any fault network, including systems of antithetic and synthetic faults. From the UVT model, a hybrid grid, containing non-cubic cells at the fault locations to honor both faults and stratigraphy, is created. These hybrid meshes are numerically efficient compared to pure tetrahedral or hexahedral meshes as the “non-hexahedral” elements are in topological continuity with non-faulted hexahedral neighbors.

As the hybrid grid is created from a UVT model, the relationship of every mesh node with the UVT is maintained. The fully unstructured mesh supporting the UVT model is restored at the same time as the hybrid grid. Also, the hybrid grid is created in the UVT space so eroded parts of the hybrid grid can be constructed as well, and then be given to the basin simulation software for pre-erosion computations.

Putting it all together

The illustration shows the sequential restoration of a UVT model and its associated hybrid grid as input data to basin modeling software. Each step is a layer removal followed by a flattening of the top of layer. Faults are kept in contact while the top layer is flattened.

From top to base (example from a synthetic model built from sandbox experiment): (A) geometry at current time (B) geometry at deposition time of the green unit (C) geometry before deposition of the green unit (D) geometry at the deposition of the blue unit.

The UVT transform enables the construction of 4D basin model geometry like never before. The 3D restoration of a UVT model is as easy as the construction of the UVT model because the unstructured mesh of the UVT is reused fully for the 3D restoration. The 4D model becomes a sequence of restored UVT models, where material eroded through time, also computed by the UVT transform, can be added. As the UVT model is restored, a hybrid grid generated in the UVT model is restored for the basin simulation to run forward simulations.

The combination of the UVT transform and 3D restoration is a large step forward in 3D restoration for structural model analysis. The new generation of hybrid grids from a UVT model has direct applications not only in basin modeling, but also in coupled geomechanical and flow-simulations.

References

Dulac, J.C. et Al. (2008) The need for a correct geological modelling support: the advent of the UVT-transform, First Break

Gringarten, E. et Al. (2008) New Grids for Robust Reservoir Modeling, SPE Publications

Mallet, J.L. (2004) Geomodelling, Oxford University Press.

Mallet, J.L. (2008) Numerical Earth Models, EAGE Publications.

Moretti, I. et Al. (2006) KINE3D: A New 3D Restoration Method Based on a Mixed Approach Linking Geometry and Geomechanics, Oil and Gas Science and Technology

Rudkiewicz, J.L. et Al. (2000) Integrated Basin Modeling Helps to Decipher Petroleum Systems, AAPG publications